Example 7 - Refining a triangulation
Contents
Example 7 - Refining a triangulation¶
We have seen how the standard meshes can be uniformly refined to finer resolution. The routines used for this task are available to the stripy user for non-uniform refinement as well.
Notebook contents¶
import stripy as stripy
import numpy as np
Uniform meshes by refinement¶
The refinement_level parameter of the stripy meshes makes repeated loops determining the bisection points of all the existing edges in the triangulation and then creating a new triangulation that includes these points and the original ones. These refinement operations can also be used for non-uniform refinement.
ico0 = stripy.spherical_meshes.icosahedral_mesh(refinement_levels=0)
ico1 = stripy.spherical_meshes.icosahedral_mesh(refinement_levels=1)
ico2 = stripy.spherical_meshes.icosahedral_mesh(refinement_levels=2)
ico3 = stripy.spherical_meshes.icosahedral_mesh(refinement_levels=3)
ico4 = stripy.spherical_meshes.icosahedral_mesh(refinement_levels=4)
ico5 = stripy.spherical_meshes.icosahedral_mesh(refinement_levels=5)
ico6 = stripy.spherical_meshes.icosahedral_mesh(refinement_levels=6)
ico7 = stripy.spherical_meshes.icosahedral_mesh(refinement_levels=7)
print("Size of mesh - 1 {}".format(ico1.points.shape[0]))
print("Size of mesh - 2 {}".format(ico2.points.shape[0]))
print("Size of mesh - 3 {}".format(ico3.points.shape[0]))
print("Size of mesh - 4 {}".format(ico4.points.shape[0]))
print("Size of mesh - 5 {}".format(ico5.points.shape[0]))
print("Size of mesh - 6 {}".format(ico6.points.shape[0]))
print("Size of mesh - 7 {}".format(ico7.points.shape[0]))
Size of mesh - 1 42
Size of mesh - 2 162
Size of mesh - 3 642
Size of mesh - 4 2562
Size of mesh - 5 10242
Size of mesh - 6 40962
Size of mesh - 7 163842
Refinement strategies¶
Five refinement strategies:
Bisect all segments connected to a given node
Refine all triangles connected to a given node by adding a point at the centroid or bisecting all edges
Refune a given triangle by adding a point at the centroid or bisecting all edges
These are provided as follows:
mlons, mlats = ico3.midpoint_refine_triangulation_by_vertices(vertices=[1,2,3,4,5,6,7,8,9,10])
ico3mv = stripy.sTriangulation(mlons, mlats)
mlons, mlats = ico3.edge_refine_triangulation_by_vertices(vertices=[1,2,3,4,5,6,7,8,9,10])
ico3ev = stripy.sTriangulation(mlons, mlats)
mlons, mlats = ico3.centroid_refine_triangulation_by_vertices(vertices=[1,2,3,4,5,6,7,8,9,10])
ico3cv = stripy.sTriangulation(mlons, mlats)
mlons, mlats = ico3.edge_refine_triangulation_by_triangles(triangles=[1,2,3,4,5,6,7,8,9,10])
ico3et = stripy.sTriangulation(mlons, mlats)
mlons, mlats = ico3.centroid_refine_triangulation_by_triangles(triangles=[1,2,3,4,5,6,7,8,9,10])
ico3ct = stripy.sTriangulation(mlons, mlats)
print (ico3mv.npoints, ico3mv.simplices.shape[0])
print (ico3ev.npoints, ico3ev.simplices.shape[0])
print (ico3cv.npoints, ico3cv.simplices.shape[0])
print (ico3et.npoints, ico3et.simplices.shape[0])
print (ico3ct.npoints, ico3ct.simplices.shape[0])
692 1380
742 1480
692 1380
664 1324
652 1300
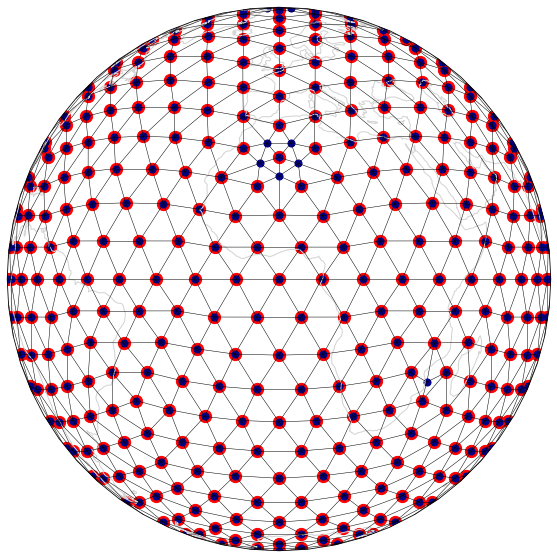
Visualisation of refinement strategies¶
import matplotlib.pyplot as plt
%matplotlib inline
import cartopy
import cartopy.crs as ccrs
def mesh_fig(mesh, meshR, name):
fig = plt.figure(figsize=(10, 10), facecolor="none")
ax = plt.subplot(111, projection=ccrs.Orthographic(central_longitude=0.0, central_latitude=0.0, globe=None))
ax.coastlines(color="lightgrey")
ax.set_global()
generator = mesh
refined = meshR
lons0 = np.degrees(generator.lons)
lats0 = np.degrees(generator.lats)
lonsR = np.degrees(refined.lons)
latsR = np.degrees(refined.lats)
lst = refined.lst
lptr = refined.lptr
ax.scatter(lons0, lats0, color="Red",
marker="o", s=150.0, transform=ccrs.PlateCarree())
ax.scatter(lonsR, latsR, color="DarkBlue",
marker="o", s=50.0, transform=ccrs.PlateCarree())
segs = refined.identify_segments()
for s1, s2 in segs:
ax.plot( [lonsR[s1], lonsR[s2]],
[latsR[s1], latsR[s2]],
linewidth=0.5, color="black", transform=ccrs.Geodetic())
fig.savefig(name, dpi=250, transparent=True)
return
mesh_fig(ico3, ico3mv, "EdgeByVertex1to10" )
mesh_fig(ico3, ico3ev, "EdgeByVertexT1to10" )
mesh_fig(ico3, ico3cv, "CentroidByVertexT1to10" )
mesh_fig(ico3, ico3et, "EdgeByTriangle1to10" )
mesh_fig(ico3, ico3ct, "CentroidByTriangle1to10" )
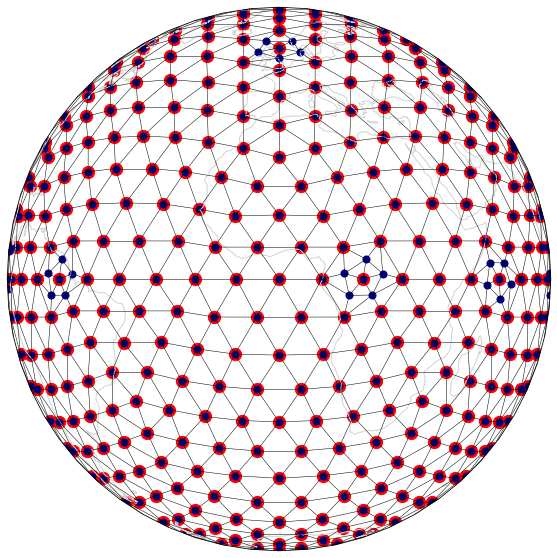
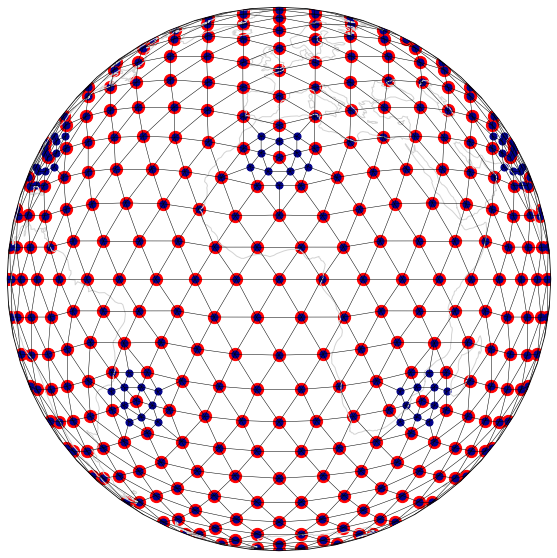
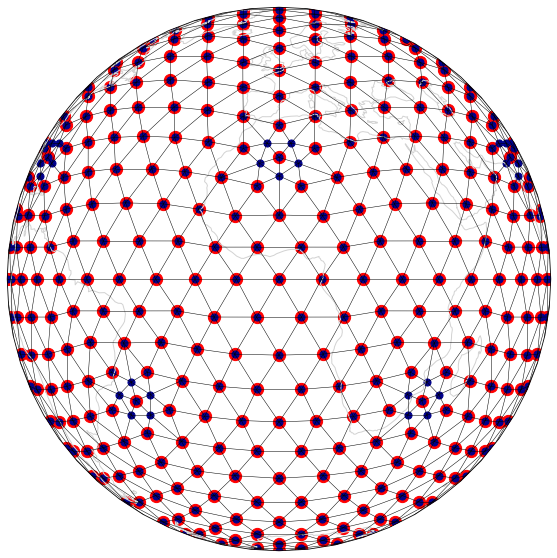
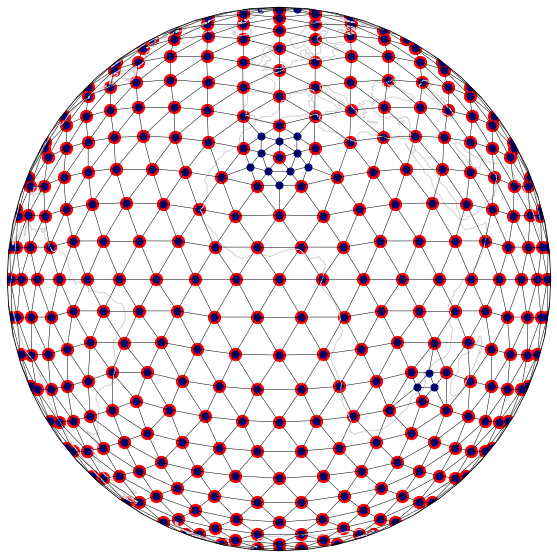
Targetted refinement¶
Here we refine a triangulation to a specific criterion - resolving two points in distinct triangles or with distinct nearest neighbour vertices.
points = np.array([[ 0.03, 0.035], [0.05, 0.055]]).T
triangulations = [ico1]
nearest, distances = triangulations[-1].nearest_vertex(points[:,0], points[:,1])
max_depth = 15
while nearest[0] == nearest[1] and max_depth > 0:
lons, lats = triangulations[-1].centroid_refine_triangulation_by_vertices(vertices=nearest[0])
new_triangulation = stripy.sTriangulation(lons, lats)
nearest, distances = new_triangulation.nearest_vertex(points[:,0], points[:,1])
triangulations.append(new_triangulation)
max_depth -= 1
print ("refinement_steps =", len(triangulations))
centroid_triangulations = triangulations[:]
refinement_steps = 5
triangulations = [ico1]
nearest, distances = triangulations[-1].nearest_vertex(points[:,0], points[:,1])
max_depth = 15
while nearest[0] == nearest[1] and max_depth > 0:
lons, lats = triangulations[-1].edge_refine_triangulation_by_vertices(vertices=nearest[0])
new_triangulation = stripy.sTriangulation(lons, lats)
nearest, distances = new_triangulation.nearest_vertex(points[:,0], points[:,1])
triangulations.append(new_triangulation)
max_depth -= 1
print ("refinement_steps =", len(triangulations))
edge_triangulations = triangulations[:]
refinement_steps = 6
triangulations = [ico1]
in_triangle = triangulations[-1].containing_triangle(points[:,0], points[:,1])
max_depth = 100
while in_triangle[0] == in_triangle[1] and max_depth > 0:
lons, lats = triangulations[-1].edge_refine_triangulation_by_triangles(in_triangle[0])
new_triangulation = stripy.sTriangulation(lons, lats)
in_triangle = new_triangulation.containing_triangle(points[:,0], points[:,1])
triangulations.append(new_triangulation)
print (in_triangle)
if in_triangle.shape[0] == 0:
break
max_depth -= 1
print ("refinement_steps =", len(triangulations))
edge_t_triangulations = triangulations[:]
[85 85]
[90 90]
[92 92]
[102 102]
[104 104]
[111 106]
refinement_steps = 7
triangulations = [ico1]
in_triangle = triangulations[-1].containing_triangle(points[:,0], points[:,1])
max_depth = 100
while in_triangle[0] == in_triangle[1] and max_depth > 0:
lons, lats = triangulations[-1].centroid_refine_triangulation_by_triangles(in_triangle[0])
new_triangulation = stripy.sTriangulation(lons, lats)
in_triangle = new_triangulation.containing_triangle(points[:,0], points[:,1])
triangulations.append(new_triangulation)
print (in_triangle)
if in_triangle.shape[0] == 0:
break
max_depth -= 1
print ("refinement_steps =", len(triangulations))
centroid_t_triangulations = triangulations[:]
[63 63]
[70 70]
[85 85]
[64 64]
[87 87]
[91 91]
[92 92]
[92 92]
[96 96]
[99 97]
refinement_steps = 11
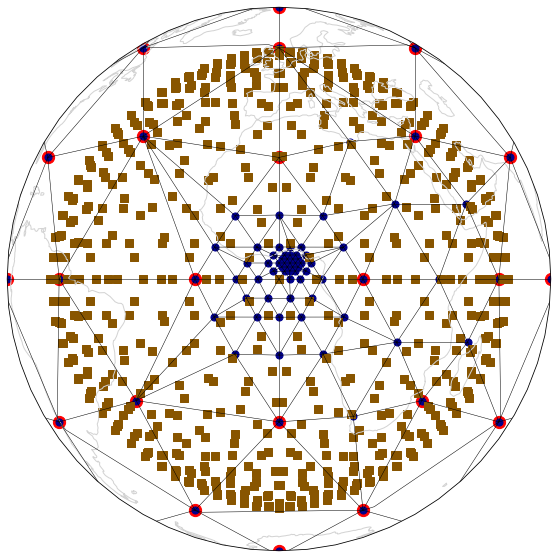
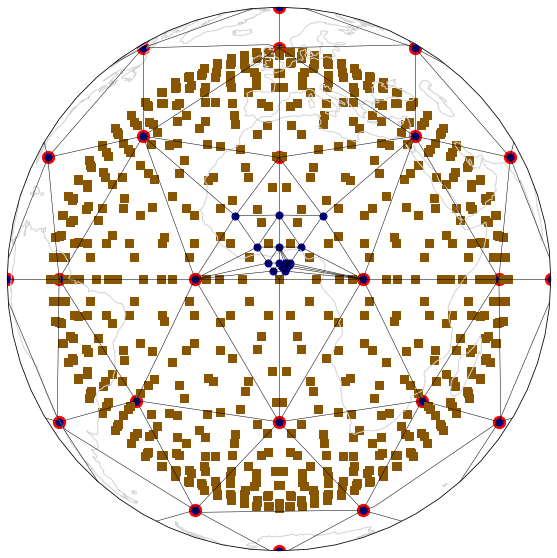
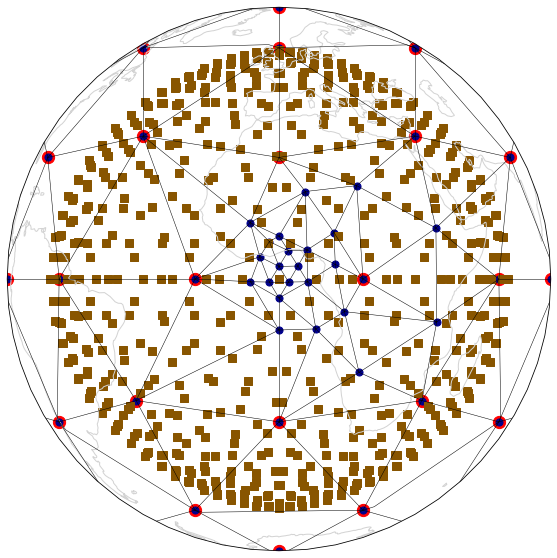
Visualisation of targetted refinement¶
import k3d
## The four different triangulation strategies
t = [ edge_triangulations[-1],
edge_t_triangulations[-1],
centroid_triangulations[-1],
centroid_t_triangulations[-1] ]
plot = k3d.plot(camera_auto_fit=False, grid_visible=False,
menu_visibility=True, axes_helper=False )
mesh_viewer = []
wire_viewer = []
for i in range(0,4):
indices = t[i].simplices.astype(np.uint32)
points = np.column_stack(t[i].points.T).astype(np.float32)
mesh_viewer.append(k3d.mesh(points, indices, wireframe=False,
color=0x99AABB,
name="mesh viewer {}".format(i+1),
flat_shading=True, opacity=1.0 ))
wire_viewer.append(k3d.mesh(points, indices, wireframe=True,
color=0x002244,
name="wire frame viewer {}".format(i+1),
flat_shading=True, opacity=1.0 ))
plot += mesh_viewer[i]
plot += wire_viewer[i]
## This helps to manage the wireframe / transparency
indices = ico3.simplices.astype(np.uint32)
points = np.column_stack(ico3.points.T).astype(np.float32)
background = k3d.mesh(points*0.9, indices, wireframe=False,
color=0xBBBBBB, opacity=1.0, flat_shading=False )
plot += background
plot.display()
## ## ##
from ipywidgets import interact, interactive
import ipywidgets as widgets
choices = { "edge triangulation": 0,
"edge t triangulation": 1,
"centroid triangulation": 2,
"centroid t triangulation": 3 }
@interact(choice=choices.keys())
def chooser(choice):
for i in range(0,4):
mesh_viewer[i].visible = False
wire_viewer[i].visible = False
mesh_viewer[choices[choice]].visible = True
wire_viewer[choices[choice]].visible = True
return
import matplotlib.pyplot as plt
%matplotlib inline
import cartopy
import cartopy.crs as ccrs
def mesh_fig(mesh, meshR, name):
fig = plt.figure(figsize=(10, 10), facecolor="none")
ax = plt.subplot(111, projection=ccrs.Orthographic(central_longitude=0.0, central_latitude=0.0, globe=None))
ax.coastlines(color="lightgrey")
ax.set_global()
generator = mesh
refined = meshR
lons0 = np.degrees(generator.lons)
lats0 = np.degrees(generator.lats)
lonsR = np.degrees(refined.lons)
latsR = np.degrees(refined.lats)
ax.scatter(lons0, lats0, color="Red",
marker="o", s=150.0, transform=ccrs.PlateCarree())
ax.scatter(lonsR, latsR, color="DarkBlue",
marker="o", s=50.0, transform=ccrs.PlateCarree())
ax.scatter(np.degrees(points[:,0]), np.degrees(points[:,1]), marker="s", s=50,
color="#885500", transform=ccrs.PlateCarree())
segs = refined.identify_segments()
for s1, s2 in segs:
ax.plot( [lonsR[s1], lonsR[s2]],
[latsR[s1], latsR[s2]],
linewidth=0.5, color="black", transform=ccrs.Geodetic())
fig.savefig(name, dpi=250, transparent=True)
return
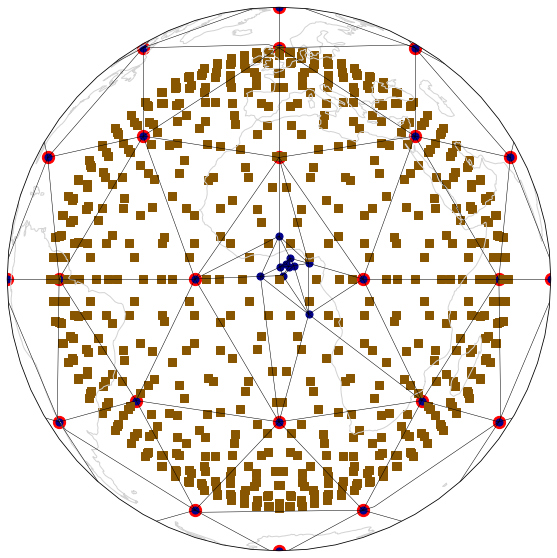
mesh_fig(edge_triangulations[0], edge_triangulations[-1], "EdgeByVertex" )
T = edge_triangulations[-1]
E = np.array(T.edge_lengths()).T
A = np.array(T.areas()).T
equant = np.max(E, axis=1) / np.min(E, axis=1)
size_ratio = np.sqrt(np.max(A) / np.min(A))
print ("EBV", T.simplices.shape[0], equant.max(), equant.min(), size_ratio)
mesh_fig(edge_t_triangulations[0], edge_t_triangulations[-1], "EdgeByTriangle" )
T = edge_t_triangulations[-1]
E = np.array(T.edge_lengths()).T
A = np.array(T.areas()).T
equant = np.max(E, axis=1) / np.min(E, axis=1)
size_ratio = np.sqrt(np.max(A) / np.min(A))
print ("EBT", T.simplices.shape[0], equant.max(), equant.min(), size_ratio)
mesh_fig(centroid_triangulations[0], centroid_triangulations[-1], "CentroidByVertex" )
T = centroid_triangulations[-1]
E = np.array(T.edge_lengths()).T
A = np.array(T.areas()).T
equant = np.max(E, axis=1) / np.min(E, axis=1)
size_ratio = np.sqrt(np.max(A) / np.min(A))
print ("CBV", T.simplices.shape[0], equant.max(), equant.min(), size_ratio)
mesh_fig(centroid_t_triangulations[0], centroid_t_triangulations[-1], "CentroidByTriangle" )
T = centroid_t_triangulations[-1]
E = np.array(T.edge_lengths()).T
A = np.array(T.areas()).T
equant = np.max(E, axis=1) / np.min(E, axis=1)
size_ratio = np.sqrt(np.max(A) / np.min(A))
print ("CBT", T.simplices.shape[0], equant.max(), equant.min(), size_ratio)
EBV 200 4.540084060033664 1.0 35.2792941304391
EBT 116 32.054115598497226 1.0 69.26762587558879
CBV 126 2.89224779940056 1.0 11.691555217725488
CBT 100 3.4282922914052634 1.0 32.74941535800478
The next example is Ex8-Spline-Tension