Example 5 - stripy smoothing operations
Contents
Example 5 - stripy smoothing operations¶
SRFPACK is a Fortran 77 software package that constructs a smooth interpolatory or approximating surface to data values associated with arbitrarily distributed points. It employs automatically selected tension factors to preserve shape properties of the data and avoid overshoot and undershoot associated with steep gradients.
Here we demonstrate how to access SRFPACK smoothing through the stripy interface.
Notebook contents¶
The next example is Ex6-Scattered-Data
Define a computational mesh¶
Use the (usual) icosahedron with face points included.
import stripy as stripy
xmin = 0.0
xmax = 10.0
ymin = 0.0
ymax = 10.0
extent = [xmin, xmax, ymin, ymax]
spacingX = 0.2
spacingY = 0.2
mesh = stripy.cartesian_meshes.elliptical_mesh(extent, spacingX, spacingY, refinement_levels=1)
mesh = stripy.Triangulation(mesh.x, mesh.y, permute=True)
print(mesh.npoints)
1744
Analytic function with noise and short wavelengths¶
Define a relatively smooth function that we can interpolate from the coarse mesh to the fine mesh and analyse
import numpy as np
def analytic(xs, ys, k1, k2):
return np.cos(k1*xs) * np.sin(k2*ys)
def analytic_noisy(xs, ys, k1, k2, noise, short):
return np.cos(k1*xs) * np.sin(k2*ys) + \
short * (np.cos(k1*5.0*xs) * np.sin(k2*5.0*ys)) + \
noise * np.random.random(xs.shape)
# def analytic_ddlon(xs, ys, k1, k2):
# return -k1 * np.sin(k1*xs) * np.sin(k2*ys) / np.cos(ys)
# def analytic_ddlat(xs, ys, k1, k2):
# return k2 * np.cos(k1*xs) * np.cos(k2*ys)
analytic_sol = analytic(mesh.x, mesh.y, 0.1, 1.0)
analytic_sol_n = analytic_noisy(mesh.x, mesh.y, 0.1, 1.0, 0.2, 0.0)
%matplotlib inline
import matplotlib.pyplot as plt
def axis_mesh_field(fig, ax, mesh, field, label):
ax.axis('off')
x0 = mesh.x
y0 = mesh.y
trip = ax.tripcolor(x0, y0, mesh.simplices, field, cmap=plt.cm.RdBu)
fig.colorbar(trip, ax=ax)
ax.set_title(str(label))
return
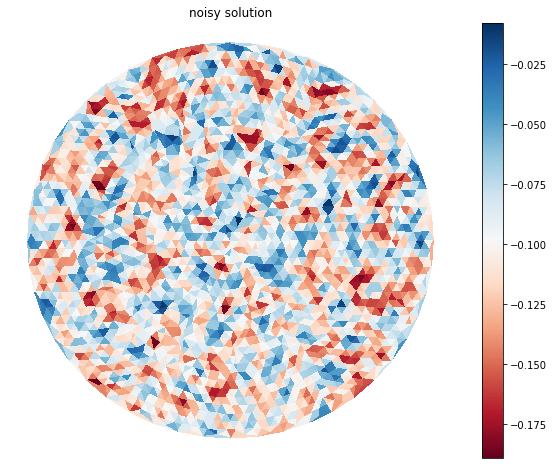
fig = plt.figure(figsize=(10, 8), facecolor="none")
ax = fig.add_subplot(111)
axis_mesh_field(fig, ax, mesh, analytic_sol-analytic_sol_n, "noisy solution")
Smoothing operations¶
The Triangulation.smoothing method directly wraps the SRFPACK smoother that smooths a surface f described
by values on the mesh vertices to find a new surface f’ (also described on the mesh vertices) by choosing nodal function values and gradients to minimize the linearized curvature of F subject to a bound on the deviation from the data values.
help(mesh.smoothing)
Help on method smoothing in module stripy.cartesian:
smoothing(f, w, sm, smtol, gstol, sigma=None) method of stripy.cartesian.Triangulation instance
Smooths a surface `f` by choosing nodal function values and gradients to
minimize the linearized curvature of F subject to a bound on the
deviation from the data values. This is more appropriate than interpolation
when significant errors are present in the data.
Args:
f : array of floats, shape (n,)
field to apply smoothing on
w : array of floats, shape (n,)
weights associated with data value in `f`
`w[i] = 1/sigma_f**2` is a good rule of thumb.
sm : float
positive parameter specifying an upper bound on Q2(f).
generally `n-sqrt(2n) <= sm <= n+sqrt(2n)`
smtol : float [0,1]
specifies relative error in satisfying the constraint
`sm(1-smtol) <= Q2 <= sm(1+smtol)` between 0 and 1.
gstol : float
tolerance for convergence.
`gstol = 0.05*mean(sigma_f)**2` is a good rule of thumb.
sigma : array of floats, shape (6n-12)
precomputed array of spline tension factors from
`get_spline_tension_factors(zdata, tol=1e-3, grad=None)`
Returns:
f_smooth : array of floats, shape (n,)
smoothed version of f
derivatives : tuple of floats, shape (n,3)
\\( \partial f \partial y , \partial f \partial y \\) first derivatives
of `f_smooth` in the x and y directions
err : error indicator
0 indicates no error, +ve values indicate warnings, -ve values are errors
stripy_smoothed, dds, err = mesh.smoothing(analytic_sol_n, np.ones_like(analytic_sol_n), 10.0, 0.01, 0.01)
stripy_smoothed2, dds2, err = mesh.smoothing(analytic_sol_n, np.ones_like(analytic_sol_n), 1.0, 0.1, 0.01)
stripy_smoothed3, dds3, err = mesh.smoothing(analytic_sol_n, np.ones_like(analytic_sol_n), 20.0, 0.1, 0.01)
delta_n = analytic_sol_n - stripy_smoothed
delta_ns = analytic_sol - stripy_smoothed
delta_n2 = analytic_sol_n - stripy_smoothed2
delta_ns2 = analytic_sol - stripy_smoothed2
delta_n3 = analytic_sol_n - stripy_smoothed3
delta_ns3 = analytic_sol - stripy_smoothed3
stripy_smoothed, dds
(array([-0.70744693, -0.6404543 , -0.7550898 , ..., 0.16793136,
-0.058718 , -0.15777792], dtype=float32),
[array([ 0.05584065, 0.00837451, 0.00973142, ..., -0.02489555,
-0.00924283, -0.01793779], dtype=float32),
array([ 0.23369917, 0.39457884, 0.06610286, ..., -0.41360974,
-0.36249393, -0.30371946], dtype=float32)])
Results of smoothing with different value of sm¶
fig, ax = plt.subplots(2,2, figsize=(12, 10), facecolor="none")
axis_mesh_field(fig, ax[0,0], mesh, analytic_sol_n, label="original")
axis_mesh_field(fig, ax[0,1], mesh, stripy_smoothed, label="smoothed1")
axis_mesh_field(fig, ax[1,0], mesh, stripy_smoothed2, label="smoothed2")
axis_mesh_field(fig, ax[1,1], mesh, stripy_smoothed3, label="smoothed3")
plt.show()
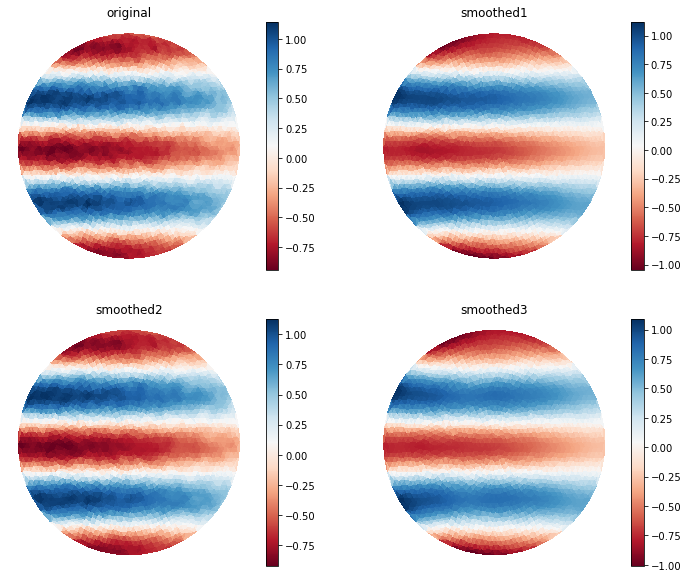
The next example is Ex6-Scattered-Data
fig, ax = plt.subplots(2,2, figsize=(12,10), facecolor="none")
axis_mesh_field(fig, ax[0,0], mesh, analytic_sol_n, label="original")
axis_mesh_field(fig, ax[0,1], mesh, dds[1], label="smoothed1")
axis_mesh_field(fig, ax[1,0], mesh, dds2[1], label="smoothed2")
axis_mesh_field(fig, ax[1,1], mesh, dds3[1], label="smoothed3")
plt.show()
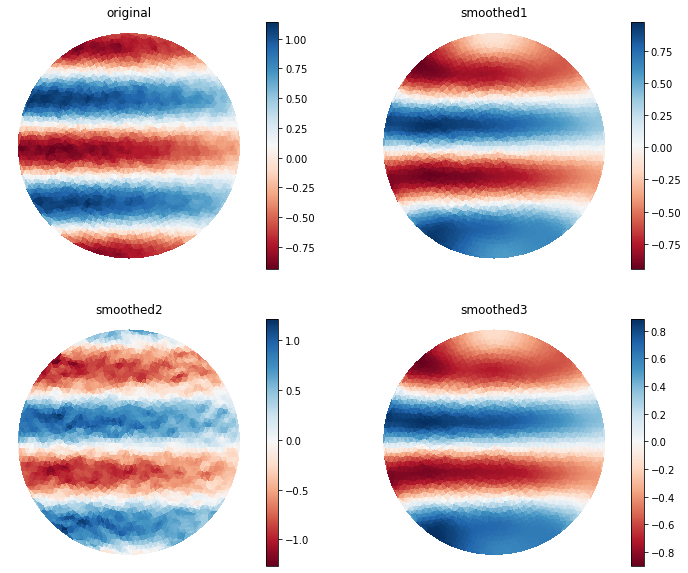
The next notebook is Ex6-Scattered-Data