Example 7 - Refining a triangulation
Contents
Example 7 - Refining a triangulation¶
We have seen how the standard meshes can be uniformly refined to finer resolution. The routines used for this task are available to the stripy user for non-uniform refinement as well.
Notebook contents¶
import stripy as stripy
import numpy as np
xmin = 0.0
xmax = 10.0
ymin = 0.0
ymax = 10.0
extent = [xmin, xmax, ymin, ymax]
spacingX = 0.5
spacingY = 0.5
Uniform meshes by refinement¶
The refinement_level parameter of the stripy meshes makes repeated loops determining the bisection points of all the existing edges in the triangulation and then creating a new triangulation that includes these points and the original ones. These refinement operations can also be used for non-uniform refinement.
ellip0 = stripy.cartesian_meshes.elliptical_mesh(extent, spacingX, spacingY, refinement_levels=0)
ellip1 = stripy.cartesian_meshes.elliptical_mesh(extent, spacingX, spacingY, refinement_levels=1)
ellip2 = stripy.cartesian_meshes.elliptical_mesh(extent, spacingX, spacingY, refinement_levels=2)
ellip3 = stripy.cartesian_meshes.elliptical_mesh(extent, spacingX, spacingY, refinement_levels=3)
ellip4 = stripy.cartesian_meshes.elliptical_mesh(extent, spacingX, spacingY, refinement_levels=4)
ellip5 = stripy.cartesian_meshes.elliptical_mesh(extent, spacingX, spacingY, refinement_levels=5)
ellip6 = stripy.cartesian_meshes.elliptical_mesh(extent, spacingX, spacingY, refinement_levels=6)
ellip7 = stripy.cartesian_meshes.elliptical_mesh(extent, spacingX, spacingY, refinement_levels=7)
print("Size of mesh - 1 {}".format(ellip1.points.shape[0]))
print("Size of mesh - 2 {}".format(ellip2.points.shape[0]))
print("Size of mesh - 3 {}".format(ellip3.points.shape[0]))
print("Size of mesh - 4 {}".format(ellip4.points.shape[0]))
print("Size of mesh - 5 {}".format(ellip5.points.shape[0]))
print("Size of mesh - 6 {}".format(ellip6.points.shape[0]))
print("Size of mesh - 7 {}".format(ellip7.points.shape[0]))
Size of mesh - 1 253
Size of mesh - 2 739
Size of mesh - 3 2197
Size of mesh - 4 6571
Size of mesh - 5 19693
Size of mesh - 6 59059
Size of mesh - 7 177157
Refinement strategies¶
Five refinement strategies:
Bisect all segments connected to a given node
Refine all triangles connected to a given node by adding a point at the centroid or bisecting all edges
Refine a given triangle by adding a point at the centroid or bisecting all edges
These are provided as follows:
mx, my = ellip2.midpoint_refine_triangulation_by_vertices(vertices=[1,2,3,4,5,6,7,8,9,10])
ellip2mv = stripy.Triangulation(mx, my)
mx, my = ellip2.edge_refine_triangulation_by_vertices(vertices=[1,2,3,4,5,6,7,8,9,10])
ellip2ev = stripy.Triangulation(mx, my)
mx, my = ellip2.centroid_refine_triangulation_by_vertices(vertices=[1,2,3,4,5,6,7,8,9,10])
ellip2cv = stripy.Triangulation(mx, my)
mx, my = ellip2.edge_refine_triangulation_by_triangles(triangles=[1,2,3,4,5,6,7,8,9,10])
ellip2et = stripy.Triangulation(mx, my)
mx, my = ellip2.centroid_refine_triangulation_by_triangles(triangles=[1,2,3,4,5,6,7,8,9,10])
ellip2ct = stripy.Triangulation(mx, my)
str_fmt = "refinement --- {} points, {} simplices"
print(str_fmt.format(ellip2mv.npoints, ellip2mv.simplices.shape[0]))
print(str_fmt.format(ellip2ev.npoints, ellip2ev.simplices.shape[0]))
print(str_fmt.format(ellip2cv.npoints, ellip2cv.simplices.shape[0]))
print(str_fmt.format(ellip2et.npoints, ellip2et.simplices.shape[0]))
print(str_fmt.format(ellip2ct.npoints, ellip2ct.simplices.shape[0]))
refinement --- 795 points, 1570 simplices
refinement --- 849 points, 1678 simplices
refinement --- 795 points, 1570 simplices
refinement --- 760 points, 1500 simplices
refinement --- 749 points, 1478 simplices
Visualisation of refinement strategies¶
%matplotlib inline
import matplotlib.pyplot as plt
def mesh_fig(mesh, meshR, name):
fig = plt.figure(figsize=(10, 10), facecolor="none")
ax = plt.subplot(111)
ax.axis('off')
generator = mesh
refined = meshR
x0 = generator.x
y0 = generator.y
xR = refined.x
yR = refined.y
ax.scatter(x0, y0, color="Red", marker="o", s=50)
ax.scatter(xR, yR, color="DarkBlue", marker="o", s=10)
ax.triplot(xR, yR, refined.simplices, color="black", linewidth=0.5)
fig.savefig(name, dpi=250, transparent=True)
return
mesh_fig(ellip2, ellip2mv, "EdgeByVertex1to10" )
mesh_fig(ellip2, ellip2ev, "EdgeByVertexT1to10" )
mesh_fig(ellip2, ellip2cv, "CentroidByVertexT1to10" )
mesh_fig(ellip2, ellip2et, "EdgeByTriangle1to10" )
mesh_fig(ellip2, ellip2ct, "CentroidByTriangle1to10" )
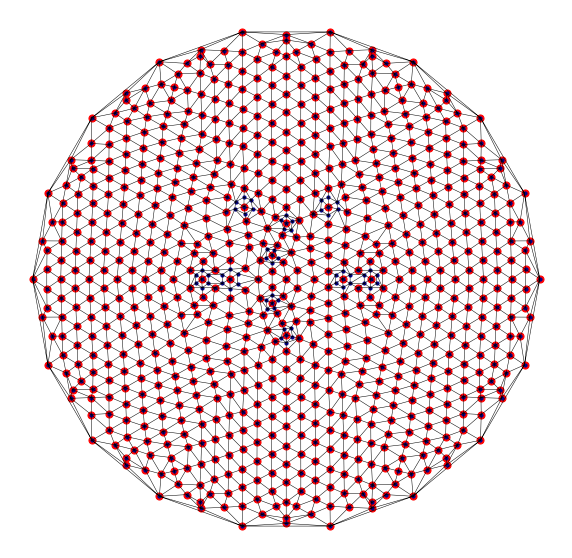
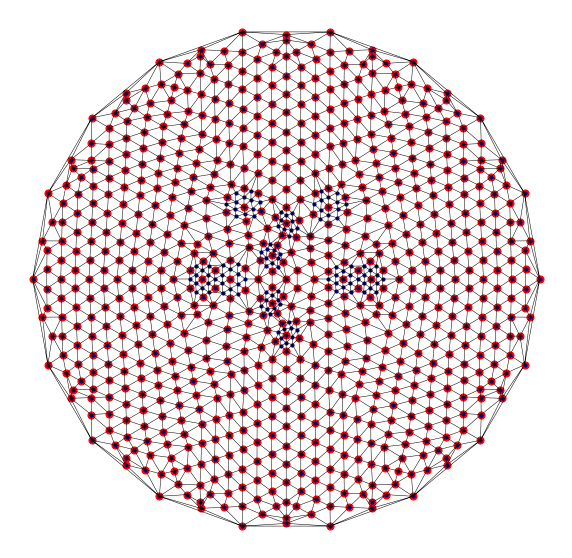
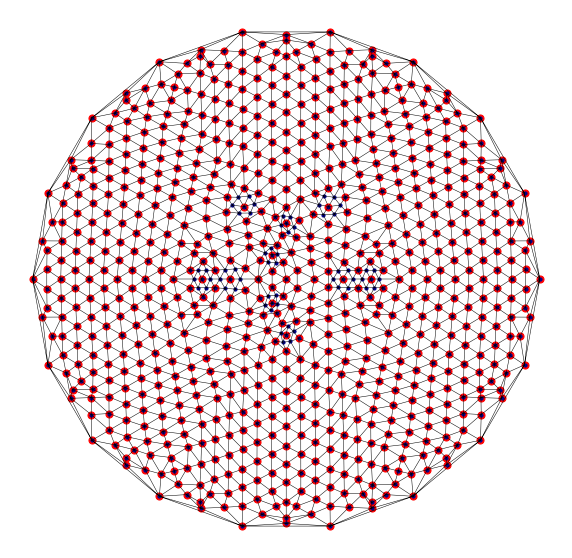
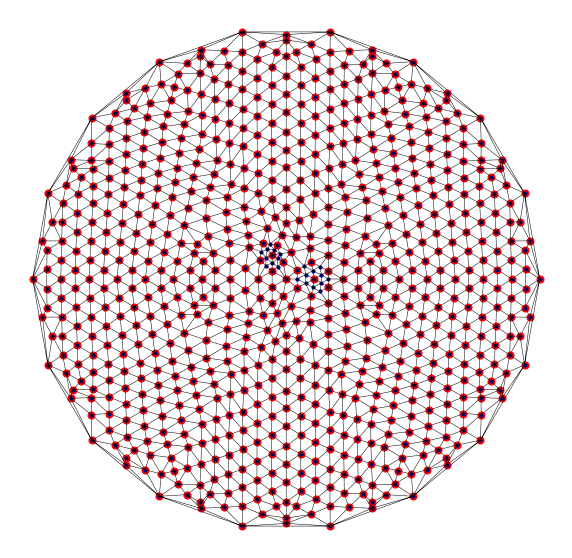
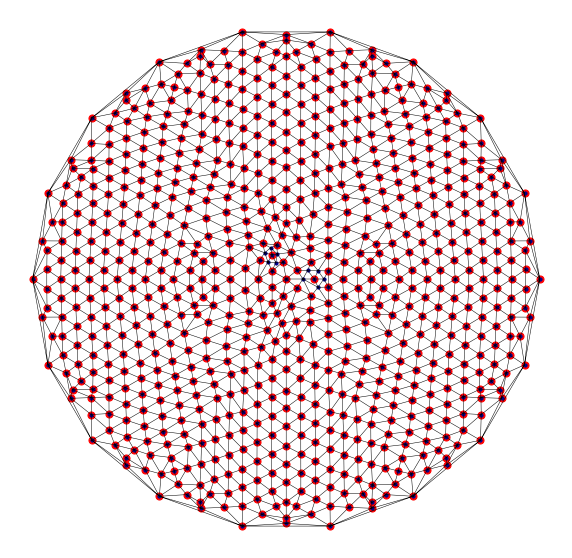
Targetted refinement¶
Here we refine a triangulation to a specific criterion - resolving two points in distinct triangles or with distinct nearest neighbour vertices.
points = np.array([[ 3.33, 3.33], [7.77, 7.77]]).T
triangulations = [ellip1]
nearest, distances = triangulations[-1].nearest_vertex(points[:,0], points[:,1])
max_depth = 10
while nearest[0] == nearest[1] and max_depth > 0:
xs, ys = triangulations[-1].centroid_refine_triangulation_by_vertices(vertices=nearest[0])
new_triangulation = stripy.Triangulation(xs, ys)
nearest, distances = new_triangulation.nearest_vertex(points[:,0], points[:,1])
triangulations.append(new_triangulation)
max_depth -= 1
print("refinement_steps = {}".format(len(triangulations)))
centroid_triangulations = triangulations[:]
refinement_steps = 11
triangulations = [ellip1]
nearest, distances = triangulations[-1].nearest_vertex(points[:,0], points[:,1])
max_depth = 10
while nearest[0] == nearest[1] and max_depth > 0:
xs, ys = triangulations[-1].edge_refine_triangulation_by_vertices(vertices=nearest[0])
new_triangulation = stripy.Triangulation(xs, ys)
nearest, distances = new_triangulation.nearest_vertex(points[:,0], points[:,1])
triangulations.append(new_triangulation)
max_depth -= 1
print("refinement_steps = {}".format(len(triangulations)))
edge_triangulations = triangulations[:]
refinement_steps = 11
triangulations = [ellip1]
in_triangle = triangulations[-1].containing_triangle(points[:,0], points[:,1])
max_depth = 10
while in_triangle[0] == in_triangle[1] and max_depth > 0:
xs, ys = triangulations[-1].edge_refine_triangulation_by_triangles(in_triangle[0])
new_triangulation = stripy.Triangulation(xs, ys)
in_triangle = new_triangulation.containing_triangle(points[:,0], points[:,1])
triangulations.append(new_triangulation)
print(in_triangle)
if in_triangle.shape[0] == 0:
break
max_depth -= 1
print("refinement_steps = {}".format(len(triangulations)))
edge_t_triangulations = triangulations[:]
[435 435]
[496 496]
[503 503]
[509 509]
[515 515]
[521 521]
[525 525]
[532 532]
[535 535]
[537 537]
refinement_steps = 11
triangulations = [ellip1]
in_triangle = triangulations[-1].containing_triangle(points[:,0], points[:,1])
max_depth = 10
while in_triangle[0] == in_triangle[1] and max_depth > 0:
xs, ys = triangulations[-1].centroid_refine_triangulation_by_triangles(in_triangle[0])
new_triangulation = stripy.Triangulation(xs, ys)
in_triangle = new_triangulation.containing_triangle(points[:,0], points[:,1])
triangulations.append(new_triangulation)
print(in_triangle)
if in_triangle.shape[0] == 0:
break
max_depth -= 1
print("refinement_steps = {}".format(len(triangulations)))
centroid_t_triangulations = triangulations[:]
[418 418]
[434 434]
[435 435]
[123 123]
[494 494]
[496 496]
[497 497]
[499 499]
[503 503]
[503 503]
refinement_steps = 11
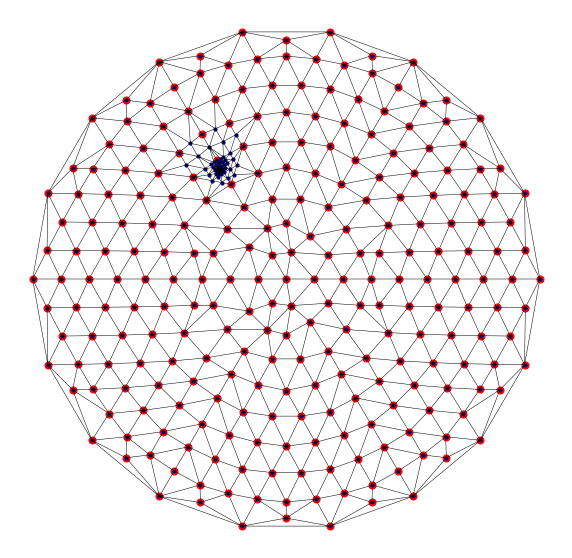
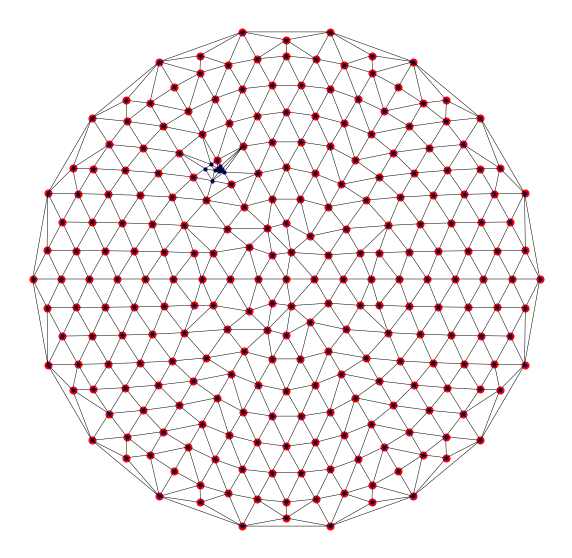
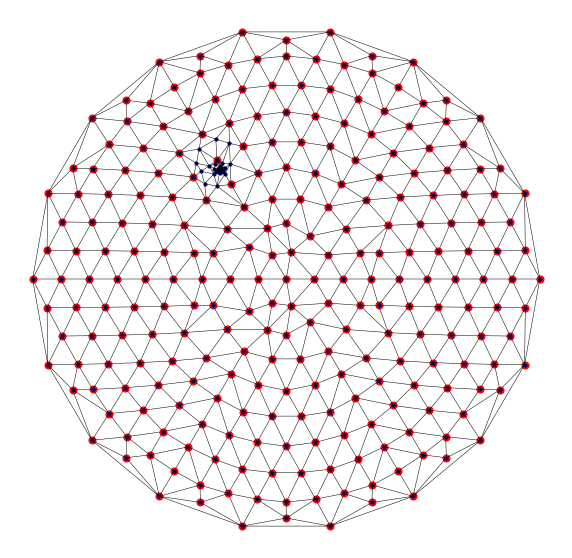
Visualisation of targetted refinement¶
import matplotlib.pyplot as plt
%matplotlib inline
str_fmt = "{:18} --- {} simplices, equant max = {:.2f}, equant min = {:.2f}, size ratio = {:.2f}"
mesh_fig(edge_triangulations[0], edge_triangulations[-1], "EdgeByVertex" )
T = edge_triangulations[-1]
E = np.array(T.edge_lengths()).T
A = np.array(T.areas()).T
equant = np.max(E, axis=1) / np.min(E, axis=1)
size_ratio = np.sqrt(np.max(A) / np.min(A))
print(str_fmt.format("EdgeByVertex", T.simplices.shape[0], equant.max(), equant.min(), size_ratio))
mesh_fig(edge_t_triangulations[0], edge_t_triangulations[-1], "EdgeByTriangle" )
T = edge_t_triangulations[-1]
E = np.array(T.edge_lengths()).T
A = np.array(T.areas()).T
equant = np.max(E, axis=1) / np.min(E, axis=1)
size_ratio = np.sqrt(np.max(A) / np.min(A))
print(str_fmt.format("EdgeByTriangle", T.simplices.shape[0], equant.max(), equant.min(), size_ratio))
mesh_fig(centroid_triangulations[0], centroid_triangulations[-1], "CentroidByVertex" )
T = centroid_triangulations[-1]
E = np.array(T.edge_lengths()).T
A = np.array(T.areas()).T
equant = np.max(E, axis=1) / np.min(E, axis=1)
size_ratio = np.sqrt(np.max(A) / np.min(A))
print(str_fmt.format("CentroidByVertex", T.simplices.shape[0], equant.max(), equant.min(), size_ratio))
mesh_fig(centroid_t_triangulations[0], centroid_t_triangulations[-1], "CentroidByTriangle" )
T = centroid_t_triangulations[-1]
E = np.array(T.edge_lengths()).T
A = np.array(T.areas()).T
equant = np.max(E, axis=1) / np.min(E, axis=1)
size_ratio = np.sqrt(np.max(A) / np.min(A))
print(str_fmt.format("CentroidByTriangle", T.simplices.shape[0], equant.max(), equant.min(), size_ratio))
EdgeByVertex --- 714 simplices, equant max = 4.20, equant min = 1.00, size ratio = 1341.99
EdgeByTriangle --- 546 simplices, equant max = 2.72, equant min = 1.00, size ratio = 1341.99
CentroidByVertex --- 600 simplices, equant max = 3.78, equant min = 1.00, size ratio = 317.88
CentroidByTriangle --- 506 simplices, equant max = 2.72, equant min = 1.00, size ratio = 68.22

The next example is Spline-Tensions